Vector expressions¶

VexCL allows the use of convenient and intuitive notation for vector operations. In order to be used in the same expression, all participating vectors have to be compatible:

Have same size;
Span same set of compute devices.

If these conditions are satisfied, then vectors may be combined with rich set of available expressions. Vector expressions are processed in parallel across all devices they were allocated on. Each vector expression results in the launch of a single compute kernel. The kernel is automatically generated and compiled the first time the expression is encountered in the program, and is submitted to command queues associated with the vector that is being assigned to.

VexCL will dump the sources of the generated kernels to stdout if either the VEXCL_SHOW_KERNELS preprocessor macro is defined, or there exists VEXCL_SHOW_KERNELS environment variable. For example, the expression:

X = 2 * Y - sin(Z);

will lead to the launch of the following compute kernel:

kernel void vexcl_vector_kernel(
    ulong n,
    global double * prm_1,
    int prm_2,
    global double * prm_3,
    global double * prm_4
)
{
    for(size_t idx = get_global_id(0); idx < n; idx += get_global_size(0)) {
        prm_1[idx] = ( ( prm_2 * prm_3[idx] ) - sin( prm_4[idx] ) );
    }
}

Here and in the rest of examples X, Y, and Z are compatible instances of vex::vector<double>; it is also assumed that OpenCL backend is selected.

VexCL is able to cache the compiled kernels offline. The compiled binaries are stored in $HOME/.vexcl on Linux and MacOSX, and in %APPDATA%\vexcl on Windows systems. In order to enable this functionality for OpenCL-based backends, the user has to define the VEXCL_CACHE_KERNELS prprocessor macro. NVIDIA OpenCL implementation does the caching already, but on AMD or Intel platforms this may lead to dramatic decrease of program initialization time (e.g. VexCL tests take around 20 seconds to complete without kernel caches, and 2 seconds when caches are available). In case of the CUDA backend the offline caching is always enabled.

VEXCL_SHOW_KERNELS¶: When defined, VexCL will dump source code of the generated kernels to stdout. Same effect may be achieved by exporting an environment variable with the same name.

VEXCL_CACHE_KERNELS¶: When defined, VexCL will use offline cache to store the compiled kernels. The first time a kernel is compiled on the system, its binaries are saved to the cache folder ($HOME/.vexcl on Unix-like systems; %APPDATA%\vexcl on Windows). Next time the program is run, the binaries will be obtained from the cache, thus speeding up the program startup.

Builtin operations¶

VexCL expressions may combine device vectors and scalars with arithmetic, logic, or bitwise operators as well as with builtin OpenCL/CUDA functions. If some builtin operator or function is unavailable, it should be considered a bug. Please do not hesitate to open an issue in this case.

Z = sqrt(2 * X) + pow(cos(Y), 2.0);

Constants¶

As you have seen above, 2 in the expression 2 * Y - sin(Z) is passed to the generated compute kernel as an int parameter (prm_2). Sometimes this is desired behaviour, because the same kernel will be reused for the expressions 42 * Z - sin(Y) or a * Y - sin(Y) (where a is an integer variable). But this may lead to a slight overhead if an expression involves true constant that will always have same value. The VEX_CONSTANT macro allows one to define such constants for use in vector expressions. Compare the generated kernel for the following example with the kernel above:

VEX_CONSTANT(two, 2);
X = two() * Y - sin(Z);

kernel void vexcl_vector_kernel(
    ulong n,
    global double * prm_1,
    global double * prm_3,
    global double * prm_4
)
{
    for(ulong idx = get_global_id(0); idx < n; idx += get_global_size(0)) {
        prm_1[idx] = ( ( ( 2 ) * prm_3[idx] ) - sin( prm_4[idx] ) );
    }
}

VexCL provides some predefined constants in the vex::constants namespace that correspond to boost::math::constants (e.g. vex::constants::pi()).

VEX_CONSTANT(name, value)¶: Creates user-defined constan functor for use in VexCL expressions. value will be copied verbatim into kernel source.

Element indices¶

The function vex::element_index() allows one to use the index of each vector element inside vector expressions. The numbering is continuous across all compute devices and starts with an optional offset.

// Linear function:
double x0 = 0.0, dx = 1.0 / (N - 1);
X = x0 + dx * vex::element_index();

// Single period of sine function:
Y = sin(vex::constants::two_pi() * vex::element_index() / N);

inline auto vex::element_index(size_t offset = 0, size_t length = 0) -> boost::proto::result_of::as_expr<elem_index, vector_domain>::type const¶: Returns index of the current element index with optional offset. Optional length parameter may be used to provide the size information to the resulting expression. This could be useful when reducing stateless expressions.

User-defined functions¶

Users may define custom functions for use in vector expressions. One has to define the function signature and the function body. The body may contain any number of lines of valid OpenCL or CUDA code, depending on the selected backend. The most convenient way to define a function is via the VEX_FUNCTION macro:

VEX_FUNCTION(double, squared_radius, (double, x)(double, y),
    return x * x + y * y;
    );
Z = sqrt(squared_radius(X, Y));

The first macro parameter here defines the function return type, the second parameter is the function name, the third parameter defines function arguments in form of a preprocessor sequence. Each element of the sequence is a tuple of argument type and name. The rest of the macro is the function body (compare this with how functions are defined in C/C++). The resulting squared_radius function object is stateless; only its type is used for kernel generation. Hence, it is safe to define commonly used functions at the global scope.

Note that any valid vector expression may be passed as a function parameter, including nested function calls:

Z = squared_radius(sin(X + Y), cos(X - Y));

Another version of the macro takes the function body directly as a string:

VEX_FUNCTION_S(double, squared_radius, (double, x)(double, y),
    "return x * x + y * y;"
    );
Z = sqrt(squared_radius(X, Y));

In case the function that is being defined calls other custom function inside its body, one can use the version of the VEX_FUNCTION macro that takes sequence of parent function names as the fourth parameter. This way the kernel generator will know to include the function definitions into the kernel source:

VEX_FUNCTION(double, bar, (double, x),
        double s = sin(x);
        return s * s;
        );
VEX_FUNCTION(double, baz, (double, x),
        double c = cos(x);
        return c * c;
        );
VEX_FUNCTION_D(double, foo, (double, x)(double, y), (bar)(baz),
        return bar(x - y) * baz(x + y);
        );

Similarly to VEX_FUNCTION_S, there is a version called VEX_FUNCTION_DS (or symmetrical VEX_FUNCTION_SD) that takes the function body as a string parameter.

Custom functions may be used not only for convenience, but also for performance reasons. The above example with squared_radius could in principle be rewritten as:

Z = sqrt(X * X + Y * Y);

The drawback of this version is that X and Y will be passed to the kernel and read twice (see the next section for an explanation).

VEX_FUNCTION(return_type, name, arguments, ...)¶

Creates a user-defined function.

The body of the function is specified as unquoted C source at the end of the macro. The source will be stringized with VEX_STRINGIZE_SOURCE macro.

VEX_FUNCTION_S(return_type, name, arguments, body)¶

Creates a user-defined function.

The body of the function is passed as a string literal or a static string expression.

VEX_FUNCTION_D(return_type, name, arguments, dependencies, ...)¶

Creates a user-defined function with dependencies.

The body of the function is specified as unquoted C source at the end of the macro. The source will be stringized with VEX_STRINGIZE_SOURCE macro.

VEX_FUNCTION_SD(return_type, name, arguments, dependencies, body)¶

Creates a user-defined function with dependencies.

The body of the function is passed as a string literal or a static string expression.

VEX_STRINGIZE_SOURCE(...)¶: Converts an unquoted text into a string literal.

Tagged terminals¶

The last example in the previous section is ineffective because the compiler cannot tell if any two terminals in an expression tree are actually referring to the same data. But programmers often have this information. VexCL allows one to pass this knowledge to compiler by tagging terminals with unique tags. By doing this, the programmer guarantees that any two terminals with matching tags are referencing the same data.

Below is a more effective variant of the above example:

using vex::tag;
Z = sqrt(tag<1>(X) * tag<1>(X) + tag<2>(Y) * tag<2>(Y));

Here, the generated kernel will have one parameter for each of the vectors X and Y:

kernel void vexcl_vector_kernel(
  ulong n,
  global double * prm_1,
  global double * prm_tag_1_1,
  global double * prm_tag_2_1
)
{
  for(ulong idx = get_global_id(0); idx < n; idx += get_global_size(0)) {
    prm_1[idx] = sqrt( ( ( prm_tag_1_1[idx] * prm_tag_1_1[idx] )
                            + ( prm_tag_2_1[idx] * prm_tag_2_1[idx] ) ) );
  }
}

template<size_t Tag, class Expr> auto vex::tag(const Expr &expr) -> const tagged_terminal<Tag, decltype(boost::proto::as_child<vector_domain>(expr))>¶

Tags terminal with a unique (in a single expression) tag.

By tagging terminals user guarantees that the terminals with same tags actually refer to the same data. VexCL is able to use this information in order to reduce number of kernel parameters and unnecessary global memory I/O operations.

Temporary values¶

Some expressions may have several occurences of the same subexpression. Unfortunately, VexCL is not able to determine these cases without the programmer’s help. For example, let us consider the following expression:

Y = log(X) * (log(X) + Z);

Here, log(X) would be computed twice. One could tag vector X as in:

auto x = vex::tag<1>(X);
Y = log(x) * (log(x) + Z);

and hope that the backend compiler is smart enough to reuse result of log(x). In fact, most modern compilers will in this simple case. But in harder cases it is possible to explicitly tell VexCL to store the result of a subexpression in a local variable and reuse it. The vex::make_temp<size_t>() function template serves this purpose:

auto tmp1 = vex::make_temp<1>( sin(X) );
auto tmp2 = vex::make_temp<2>( cos(X) );
Y = (tmp1 - tmp2) * (tmp1 + tmp2);

This will result in the following kernel:

kernel void vexcl_vector_kernel(
  ulong n,
  global double * prm_1,
  global double * prm_2_1,
  global double * prm_3_1
)
{
  for(ulong idx = get_global_id(0); idx < n; idx += get_global_size(0))
  {
    double temp_1 = sin( prm_2_1[idx] );
    double temp_2 = cos( prm_3_1[idx] );
    prm_1[idx] = ( ( temp_1 - temp_2 ) * ( temp_1 + temp_2 ) );
  }
}

Any valid vector or multivector expression (but not additive expressions, such as sparse matrix-vector products) may be wrapped into a vex::make_temp() call.

template<size_t Tag, typename T, class Expr> auto vex::make_temp(const Expr &expr) -> typename std::enable_if<boost::proto::matches<typename boost::proto::result_of::as_expr<Expr>::type, vector_expr_grammar>::value, temporary<T, Tag, typename boost::proto::result_of::as_child<const Expr, vector_domain>::type> const>::type¶

Creates temporary expression that may be reused in a vector expression.

The type of the resulting temporary variable is automatically deduced from the expression, but may also be explicitly specified as a template parameter.

Raw pointers 1 ¶

Most of the expressions in VexCL are element-wise. That is, the user describes what needs to be done on an element-by-element basis, and has no access to neighboring elements. vex::raw_pointer() allows to use pointer arithmetic with either vex::vector<T> or vex::svm_vector<T>.

The $N$-body problem

Let us consider the $N$-body problem as an example. The $N$-body problem considers $N$ point masses, $m_i,\;i=1,2,\ldots,N$ in three dimensional space $\mathbb{R}^3$ moving under the influence of mutual gravitational attraction. Each mass $m_i$ has a position vector $\vec q_i$. Newton’s law of gravity says that the gravitational force felt on mass $m_i$ by a single mass $m_j$ is given by

\[\vec F_{ij} = \frac{G m_i m_j (\vec q_j - \vec q_i)} {||\vec q_j - \vec q_i||^3},\]

where $G$ is the gravitational constant and $||\vec q_j - \vec q_i||$ is the the distance between $\vec q_i$ and $\vec q_j$.

We can find the total force acting on mass $m_i$ by summing over all masses:

\[\vec F_i = \sum\limits_{j=1,j \neq i}^N \frac{G m_i m_j (\vec q_j - \vec q_i)} {||\vec q_j - \vec q_i||^3}.\]

In VexCL, we can encode the formula above with the following custom function:

vex::vector<double>     m(ctx, n);
vex::vector<cl_double3> q(ctx, n), f(ctx, n);

VEX_FUNCTION(cl_double3, force, (size_t, n)(size_t, i)(double*, m)(cl_double3*, q),
    const double G = 6.674e-11;

    double3 sum = {0.0, 0.0, 0.0};
    double  m_i = m[i];
    double3 q_i = q[i];

    for(size_t j = 0; j < n; ++j) {
        if (j == i) continue;

        double  m_j = m[j];
        double3 d   = q[j] - q_i;
        double  r   = length(d);

        sum += G * m_i * m_j * d / (r * r * r);
    }
    return sum;
    );

f = force(n, vex::element_index(), vex::raw_pointer(m), vex::raw_pointer(q));

The function takes number of elements n, index of the current element i, and pointers to arrays of point masses m and positions q. It returns the force acting on the current point. Note that we use host-side types (cl_double3) in declaration of function return type and parameter types, and we use OpenCL types (double3) inside the function body.

Constant address space

In the OpenCL-based backends VexCL allows one to use constant cache on GPUs in order to speed up the read-only access to small vectors. Usually around 64Kb of constant cache per compute unit is available. Vectors wrapped in vex::constant() will be decorated with the constant keyword instead of the usual global one. For example, the following expression:

x = 2 * vex::constant(y);

will result in the OpenCL kernel below:

kernel void vexcl_vector_kernel(
  ulong n,
  global int * prm_1,
  int prm_2,
  constant int * prm_3
)
{
  for(ulong idx = get_global_id(0); idx < n; idx += get_global_size(0)) {
    prm_1[idx] = ( prm_2 * prm_3[idx] );
  }
}

In cases where access to arbitrary vector elements is required, vex::constant_pointer() may be used similarly to vex::raw_pointer(). The extracted pointer will be decorated with the constant keyword.

Warning

doxygenfunction: Unable to resolve function “vex::raw_pointer” with arguments (const vector<T>&) in doxygen xml output for project “VEXCL” from directory: xml. Potential matches:

- template<typename T> auto raw_pointer(const svm_vector<T> &v) -> typename boost::proto::result_of::as_expr<svm_vector_pointer<T>, vector_domain>::type
- template<typename T> auto raw_pointer(const vector<T> &v) -> typename boost::proto::result_of::as_expr<vector_pointer<T>, vector_domain>::type

Warning

doxygenfunction: Unable to resolve function “vex::raw_pointer” with arguments (const svm_vector<T>&) in doxygen xml output for project “VEXCL” from directory: xml. Potential matches:

- template<typename T> auto raw_pointer(const svm_vector<T> &v) -> typename boost::proto::result_of::as_expr<svm_vector_pointer<T>, vector_domain>::type
- template<typename T> auto raw_pointer(const vector<T> &v) -> typename boost::proto::result_of::as_expr<vector_pointer<T>, vector_domain>::type

template<class T> inline constant_vector<T> vex::constant(const vector<T> &v)¶

Uses constant cache for access to the wrapped vector.

Note

Only available for OpenCL-based backends.

template<typename T> inline auto vex::constant_pointer(const vector<T> &v) -> typename boost::proto::result_of::as_expr<constant_vector_pointer<T>, vector_domain>::type¶

Cast vex::vector to a constant pointer.

Note

Only available for OpenCL-based backends.

Random number generation¶

VexCL provides a counter-based random number generators from Random123 suite, in which N-th random number is obtained by applying a stateless mixing function to N instead of the conventional approach of using N iterations of a stateful transformation. This technique is easily parallelizable and is well suited for use in GPGPU applications.

For integral types, the generated values span the complete range; for floating point types, the generated values lie in the interval [0,1].

In order to use a random number sequence in a vector expression, the user has to declare an instance of either vex::Random or vex::RandomNormal class template as in the following example:

vex::Random<double, vex::random::threefry> rnd;

// X will contain random numbers from [-1, 1]:
X = 2 * rnd(vex::element_index(), std::rand()) - 1;

Note that vex::element_index() function here provides the random number generator with a sequence position N, and std::rand() is used to obtain a seed for this specific sequence.

Monte Carlo $\pi$

Here is a more interesting example of using random numbers to estimate the value of $\pi$. In order to do this we remember that area of a circle with radius $r$ is equal to $\pi r^2$. A square of the same ‘radius’ has area of $(2r)^2$. Then we can write

\[\frac{\text{area of circle}}{\text{area of square}} = \frac{\pi r^2}{(2r)^2} = \frac{\pi}{4},\]

\[\pi = 4 \frac{\text{area of circle}}{\text{area of square}}\]

We can estimate the last fraction in the formula above with the Monte-Carlo method. If we generate a lot of random points in a square, then ratio of circle area over square area will be approximately equal to the ratio of points in the circle over all points. This is illustrated by the following figure:

(Source code, png, hires.png, pdf)

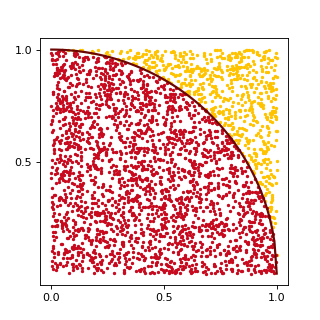
In VexCL we can compute the estimate with a single expression, that will generate single compute-bound kernel:

vex::Random<cl_double2> rnd;
vex::Reductor<size_t> sum(ctx);

double pi = sum(length(rnd(vex::element_index(0, n), std::rand())) < 1) * 4.0 / n;

Here we generate n random 2D points and use the builtin OpenCL function length to see which points are located withing the circle. Then we use the sum functor to count the points within the circle and finally multiply the number with 4.0/n to get the estimated value of $\pi$.

template<class T, class Generator = random::philox> struct Random : public vex::UserFunction<Random<T, Generator>, T(cl_ulong, cl_ulong)>¶

Returns uniformly distributed random numbers.

For integral types, generated values span the complete range.

For floating point types, generated values are in $[0,1]$.

Uses Random123 generators which provide 64(2x32), 128(4x32, 2x64) and 256(4x64) random bits, this limits the supported output types, which means cl_double8 (512bit) is not supported, but cl_uchar2 is.

Supported generator families are random::philox (based on integer multiplication, default) and random::threefry (based on the Threefish encryption function). Both satisfy rigorous statistical testing (passing BigCrush in TestU01), vectorize and parallelize well (each generator can produce at least $2^{64}$ independent streams), have long periods (the period of each stream is at least $2^{128}$), require little or no memory or state, and have excellent performance (a few clock cycles per byte of random output).

template<class T, class Generator = random::philox> struct RandomNormal : public vex::UserFunction<RandomNormal<T, Generator>, T(cl_ulong, cl_ulong)>¶

Returns normally distributed random numbers.

Uses Box-Muller transform.

Permutations 1 ¶

vex::permutation() allows the use of a permuted vector in a vector expression. The function accepts a vector expression that returns integral values (indices). The following example reverses X and assigns it to Y in two different ways:

Y = vex::permutation(n - 1 - vex::element_index())(X);

// Permutation expressions are writable!
vex::permutation(n - 1 - vex::element_index())(Y) = X;

template<class Expr> auto vex::permutation(const Expr &expr) -> typename std::enable_if<std::is_integral<typename detail::return_type<Expr>::type>::value, expr_permutation<typename boost::proto::result_of::as_child<const Expr, vector_domain>::type>>::type¶: Returns permutation functor which is based on an integral expression.

Slicing 1 ¶

An instance of the vex::slicer<NDim> class allows one to conveniently access sub-blocks of multi-dimensional arrays that are stored in vex::vector<T> in row-major order. The constructor of the class accepts the dimensions of the array to be sliced. The following example extracts every other element from interval [100, 200) of a one-dimensional vector X:

vex::vector<double> X(ctx, n);
vex::vector<double> Y(ctx, 50);

vex::slicer<1> slice(vex::extents[n]);

Y = slice[vex::range(100, 2, 200)](X);

And the example below shows how to work with a two-dimensional matrix:

using vex::range, vex::_; // vex::_ is a shortcut for an empty range

vex::vector<double> X(ctx, n * n); // n-by-n matrix stored in row-major order.
vex::vector<double> Y(ctx, n);

// vex::extents is a helper object similar to boost::multi_array::extents.
vex::slicer<2> slice(vex::extents[n][n]);

Y = slice[42](X);    // Put 42-nd row of X into Y.
Y = slice[_][42](X); // Put 42-nd column of X into Y.

slice[_][10](X) = Y; // Put Y into 10-th column of X.

// Assign sub-block [10,20)x[30,40) of X to Z:
vex::vector<double> Z = slice[range(10, 20)][range(30, 40)](X);
assert(Z.size() == 100);

template<size_t NR> struct vex::slicer¶

Slicing operator.

Provides information about shape of multidimensional vector expressions, allows to slice the expressions.

Public Functions

template<typename T> inline slicer(const std::array<T, NR> &target_dimensions)¶: Creates slicer with the given dimensions.

template<typename T> inline slicer(const T *target_dimensions)¶: Creates slicer with the given dimensions.

inline slicer(const extent_gen<NR> &ext)¶: Creates slicer with the given dimensions.

template<size_t C> struct slice : public vex::gslice<NR>¶

const extent_gen<0> vex::extents¶: Helper object for specifying slicer dimensions.

struct vex::range¶

An index range for use with slicer class.

Public Functions

inline range()¶: Unbounded range (all elements along the current dimension).

inline range(ptrdiff_t i)¶: Range with a single element.

inline range(ptrdiff_t start, ptrdiff_t stride, ptrdiff_t stop)¶: Elements from open interval with given stride.

inline range(ptrdiff_t start, ptrdiff_t stop)¶: Every element from open interval.

const range vex::_¶: Placeholder for an unbounded range.

Reducing multidimensional expressions 1 ¶

vex::reduce() function allows one to reduce a multidimensional expression along its one or more dimensions. The result is again a vector expression, which may be used in other expressions. The supported reduction operations are vex::SUM, vex::MIN, and vex::MAX. The function takes three arguments: the shape of the expression to reduce (with the slowest changing dimension in the front), the expression to reduce, and the dimension(s) to reduce along. The latter are specified as indices into the shape array. Both the shape and indices are specified as static arrays of integers, but vex::extents object may be used for convenience.

In the following example we find maximum absolute value of each row in a two-dimensional matrix and assign the result to a vector:

vex::vector<double> A(ctx, N * M);
vex::vector<double> x(ctx, N);

x = vex::reduce<vex::MAX>(vex::extents[N][M], fabs(A), vex::extents[1]);

It is also possible to use vex::slicer instance to provide information about the expression shape:

vex::slicer<2> Adim(vex::extents[N][M]);
x = vex::reduce<vex::MAX>(Adim[_](fabs(A)), vex::extents[1]);

template<class Reducer, class SlicedExpr, class ReduceDims> auto vex::reduce(const SlicedExpr &expr, const ReduceDims &reduce_dims)¶: Reduce multidimensional vector expression along specified dimensions.

template<class Reducer, class ExprShape, class Expr, class ReduceDims> auto vex::reduce(const ExprShape &shape, const Expr &expr, const ReduceDims &reduce_dims)¶: Reduce multidimensional vector expression along specified dimensions.

Reshaping 1 ¶

vex::reshape() function is a powerful primitive that allows one to conveniently manipulate multidimensional data. It takes three arguments – an arbitrary vector expression to reshape, the dimensions dst_dims of the final result (with the slowest changing dimension in the front), and the native dimensions of the expression, which are specified as indices into dst_dims. The function returns a vector expression. The dimensions may be conveniently specified with the help of vex::extents object.

Here is an example that shows how a two-dimensional matrix of size $N \times M$ could be transposed:

vex::vector<double> A(ctx, N * M);
vex::vector<double> B = vex::reshape(A,
                            vex::extents[M][N], // new shape
                            vex::extents[1][0]  // A is shaped as [N][M]
                            );

If the source expression lacks some of the destination dimensions, then those will be introduced by replicating the available data. For example, to make a two-dimensional matrix from a one-dimensional vector by copying the vector to each row of the matrix, one could do the following:

vex::vector<double> x(ctx, N);
vex::vector<double> y(ctx, M);
vex::vector<double> A(ctx, M * N);

// Copy x into each row of A:
A = vex::reshape(x, vex::extents[M][N], vex::extents[1]);
// Now, copy y into each column of A:
A = vex::reshape(y, vex::extents[M][N], vex::extents[0]);

Here is a more realistic example of a dense matrix-matrix multiplication. Elements of a matrix product $C = AB$ are defined as $C_{ij} = \sum_k A_{ik} B_{kj}$. Let’s assume that matrix $A$ has shape $N \times L$, and matrix $B$ is shaped as $L \times M$. Then matrix $C$ has dimensions $N \times M$. In order to implement the multiplication we extend matrices $A$ and $B$ to the shape of $N \times L \times M$, multiply the resulting expressions elementwise, and reduce the product along the middle dimension ($L$):

vex::vector<double> A(ctx, N * L);
vex::vector<double> B(ctx, L * M);
vex::vector<double> C(ctx, N * M);

C = vex::reduce<vex::SUM>(
        vex::extents[N][L][M],
        vex::reshape(A, vex::extents[N][L][M], vex::extents[0][1]) *
        vex::reshape(B, vex::extents[N][L][M], vex::extents[1][2]),
        1
        );

This of course would not be as efficient as a carefully crafted custom implementation or a call to a vendor BLAS function. Also, this particular operation is more efficiently done with tensor product function described in the next section.

template<class Expr, class DstDims, class SrcDims> auto vex::reshape(const Expr &expr, const DstDims &dst_dims, const SrcDims &src_dims)¶

Reshapes the expression.

Makes a multidimensional expression shaped as dst_dims from an input expression shaped as dst_dims[src_dims]. scr_dims are specified as indices into dst_dims.

Tensor product 1 ¶

Given two tensors (arrays of dimension greater than or equal to one), A and B, and a list of axes pairs (where each pair represents corresponding axes from each of the two tensors), the tensor product operation sums the products of A’s and B’s elements over the given axes. In VexCL this is implemented as vex::tensordot() operation (compare with python’s numpy.tensordot).

For example, the above matrix-matrix product may be implemented much more efficiently with vex::tensordot():

using vex::_;

vex::slicer<2> Adim(vex::extents[N][M]);
vex::slicer<2> Bdim(vex::extents[M][L]);

C = vex::tensordot(Adim[_](A), Bdim[_](B), vex::axes_pairs(1, 0));

Here instances of vex::slicer class are used to provide shape information for the A and B vectors.

template<class SlicedExpr1, size_t SlicedExpr2, size_t CDIM> auto vex::tensordot(const SlicedExpr1 &lhs, const SlicedExpr2 &rhs, const std::array<std::array<size_t, 2>, CDIM> &common_axes)¶: Tensor dot product along specified axes for multidimensional arrays.

template<class ...Args> std::array<std::array<size_t, 2>, sizeof...(Args) / 2> vex::axes_pairs(Args... args)¶

Helper function for creating axes pairs.

Example:

auto axes = axes_pairs(a0, b0, a1, b1);
assert(axes[0][0] == a0 && axes[0][1] == b0);
assert(axes[1][0] == a1 && axes[1][1] == b1);

Scattered data interpolation with multilevel B-Splines¶

VexCL provides an implementation of the MBA algorithm based on paper by Lee, Wolberg, and Shin [LeWS97]. This is a fast algorithm for scattered N-dimensional data interpolation and approximation. Multilevel B-splines are used to compute a C2-continuously differentiable surface through a set of irregularly spaced points. The algorithm makes use of a coarse-to-fine hierarchy of control lattices to generate a sequence of bicubic B-spline functions whose sum approaches the desired interpolation function. Large performance gains are realized by using B-spline refinement to reduce the sum of these functions into one equivalent B-spline function. High-fidelity reconstruction is possible from a selected set of sparse and irregular samples.

The algorithm is setup on a CPU. After that, it may be used in vector expressions. Here is an example in 2D:

// Coordinates of data points:
std::vector< std::array<double,2> > coords = {
    {0.0, 0.0},
    {0.0, 1.0},
    {1.0, 0.0},
    {1.0, 1.0},
    {0.4, 0.4},
    {0.6, 0.6}
};

// Data values:
std::vector<double> values = {
    0.2, 0.0, 0.0, -0.2, -1.0, 1.0
};

// Bounding box:
std::array<double, 2> xmin = {-0.01, -0.01};
std::array<double, 2> xmax = { 1.01,  1.01};

// Initial grid size:
std::array<size_t, 2> grid = {5, 5};

// Algorithm setup.
vex::mba<2> surf(ctx, xmin, xmax, coords, values, grid);

// x and y are coordinates of arbitrary 2D points
// (here the points are placed on a regular grid):
vex::vector<double> x(ctx, n*n), y(ctx, n*n), z(ctx, n*n);

auto I = vex::element_index() % n;
auto J = vex::element_index() / n;
vex::tie(x, y) = std::make_tuple(h * I, h * J);

// Get interpolated values:
z = surf(x, y);

LeWS97: S. Lee, G. Wolberg, and S. Y. Shin. Scattered data interpolation with multilevel B-Splines. IEEE Transactions on Visualization and Computer Graphics, 3:228–244, 1997

template<size_t NDIM, typename real = double> class vex::mba¶

Scattered data interpolation with multilevel B-Splines.

Public Functions

inline mba(const std::vector<backend::command_queue> &queue, const point &cmin, const point &cmax, const std::vector<point> &coo, std::vector<real> val, std::array<size_t, NDIM> grid, size_t levels = 8, real tol = 1e-8)¶: Creates the approximation functor. cmin and cmax specify the domain boundaries, coo and val contain coordinates and values of the data points. grid is the initial control grid size. The approximation hierarchy will have at most levels and will stop when the desired approximation precision tol will be reached.

template<class CooIter, class ValIter> inline mba(const std::vector<backend::command_queue> &queue, const point &cmin, const point &cmax, CooIter coo_begin, CooIter coo_end, ValIter val_begin, std::array<size_t, NDIM> grid, size_t levels = 8, real tol = 1e-8)¶: Creates the approximation functor. cmin and cmax specify the domain boundaries. Coordinates and values of the data points are passed as iterator ranges. grid is the initial control grid size. The approximation hierarchy will have at most levels and will stop when the desired approximation precision tol will be reached.

template<class ...Expr> inline auto operator()(const Expr&... expr) const -> mba_interp<mba, boost::tuple<const Expr&...>>¶: Provide interpolated values at given coordinates.

Fast Fourier Transform 1 ¶

VexCL provides an implementation of the Fast Fourier Transform (FFT) that accepts arbitrary vector expressions as input, allows one to perform multidimensional transforms (of any number of dimensions), and supports arbitrary sized vectors:

vex::FFT<double, cl_double2> fft(ctx, n);
vex::FFT<cl_double2, double> ifft(ctx, n, vex::fft::inverse);

vex::vector<double> rhs(ctx, n), u(ctx, n), K(ctx, n);

// Solve Poisson equation with FFT:
u = ifft( K * fft(rhs) );

template<typename Tin, typename Tout = Tin, class Planner = fft::planner> struct vex::FFT¶

Fast Fourier Transform.

FFT always works with complex types (cl_double2 or cl_float2) internally. When the input is specified as real (float or double), it is extended to the complex plane (by setting the imaginary part to zero). When user asks the output to be real, the complex values are truncated by dropping the imaginary part.

Usage:

FFT<cl_double2> fft(ctx, length);
output = fft(input); // out-of-place transform
data = fft(data);    // in-place transform
FFT<cl_double2> ifft({width, height}, fft::inverse); // implicit context
input = ifft(output); // backward transform

To batch multiple transformations, use fft::none as the first kind:

FFT<cl_double2> fft({batch, n}, {fft::none, fft::forward});
output = fft(input);

Public Functions

inline FFT(const std::vector<backend::command_queue> &queues, size_t length, fft::direction dir = fft::forward, const Planner &planner = Planner())¶: 1D constructor

inline FFT(const std::vector<backend::command_queue> &queues, const std::vector<size_t> &lengths, fft::direction dir = fft::forward, const Planner &planner = Planner())¶: N-dimensional constructor.

inline FFT(const std::vector<size_t> &lengths, fft::direction dir = fft::forward, const Planner &planner = Planner())¶: N-dimensional constructor.

inline FFT(const std::vector<backend::command_queue> &queues, const std::vector<size_t> &lengths, const std::vector<fft::direction> &dirs, const Planner &planner = Planner())¶: N-dimensional constructor.

inline FFT(const std::vector<size_t> &lengths, const std::vector<fft::direction> &dirs, const Planner &planner = Planner())¶: N-dimensional constructor.

inline FFT(const std::vector<backend::command_queue> &queues, const std::initializer_list<size_t> &lengths, fft::direction dir = fft::forward, const Planner &planner = Planner())¶: N-dimensional constructor.

inline FFT(const std::initializer_list<size_t> &lengths, fft::direction dir = fft::forward, const Planner &planner = Planner())¶: N-dimensional constructor.

inline FFT(const std::vector<backend::command_queue> &queues, const std::initializer_list<size_t> &lengths, const std::initializer_list<fft::direction> &dirs, const Planner &planner = Planner())¶: N-dimensional constructor.

inline FFT(const std::initializer_list<size_t> &lengths, const std::initializer_list<fft::direction> &dirs, const Planner &planner = Planner())¶: N-dimensional constructor.

template<class Expr> inline auto operator() (const Expr &x) -> decltype(plan.template apply< Tout >(x)): Performs the transform.

enum vex::fft::direction¶

FFT direction.

Values:

enumerator forward¶: Forward transform.

enumerator inverse¶: Inverse transform.

enumerator none¶: Specifies dimension(s) to do batch transform.

1(1,2,3,4,5,6,7): This operation involves access to arbitrary elements of its subexpressions and may lead to unpredictable device-to-device communication. Hence, it is restricted to single-device expressions. That is, only vectors that are located on a single device are allowed to participate in this operation.

Vector expressions¶

Builtin operations¶

Constants¶

Element indices¶

User-defined functions¶

Tagged terminals¶

Temporary values¶

Raw pointers 1¶

Random number generation¶

Permutations 1¶

Slicing 1¶

Reducing multidimensional expressions 1¶

Reshaping 1¶

Tensor product 1¶

Scattered data interpolation with multilevel B-Splines¶

Fast Fourier Transform 1¶

Raw pointers 1 ¶

Permutations 1 ¶

Slicing 1 ¶

Reducing multidimensional expressions 1 ¶

Reshaping 1 ¶

Tensor product 1 ¶

Fast Fourier Transform 1 ¶